MATEMÁTICA INSTRUMENTAL
A temperatura de uma determinada região sofre uma variação segundo a função T(t) = (5/7)t2 -(60/7)t +40. Em que t refere-se a certo mês do anos %7D) sendo t= 1, referente à janeiro, t= 2, referente à fevereiro... e, T(t), a temperatura em graus Celsius.
sendo t= 1, referente à janeiro, t= 2, referente à fevereiro... e, T(t), a temperatura em graus Celsius.
O valor que mais se aproxima da temperatura dessa região no mês de maio é exatamente:
25°.
13°.
10°.
8°.
15°.
Uma equação modular é toda equação cuja incógnita se apresenta em módulo, considere a equação a seguir
O conjunto solução que satisfaz a equação é dado por:
S = { } (vazio)
S = {-3, -1, 2, 3}
S = {-3, -2, 1, 2}
S = {-1, 1, 2}
S = {-2, 1, 2}
A população da bactéria de uma colônia E. coli dobra a cada 20 minutos. Em um experimento, colocou-se, inicialmente em um tubo de ensaio, uma amostra com 1000 bactérias por milímetro. No final do experimento obteve -se um total de 4,096 . 106 bactérias por milímetro.
Assim sendo, o tempo do experimento foi de
2 horas e 40 minutos.
3 horas.
3 horas e 20 minutos.
3 horas e 40 minutos.
4 horas.
O número de bactérias de certa cultura aumenta exponencialmente conforme a lei de formação %7D%3D%7BQ%7D_%7B%7B0%7D%7D.%7B%7Be%7D%7D%5E%7B%7B%7Bk%7D%7Bt%7D%7D%7D) , onde
, onde  é a quantidade inicial de bactérias ,
é a quantidade inicial de bactérias ,  o número irracional , k é uma constante e t o tempo, em horas, após o início do experimento.
o número irracional , k é uma constante e t o tempo, em horas, após o início do experimento.
Considerando k = 2.
Se uma cultura tem inicialmente 10000 bactérias então 1h depois, terá aproximadamente:
62046 bactérias
39206 bactérias
73891 bactérias
80312 bactérias
100002 bactérias
Dada a matriz, ![[[2, 5, 1],[-1, 4, -3],[3, 0, 2]]](http://sga.uniube.br/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7B%5Cleft%5B%5Cmatrix%7B%7B2%7D%26%7B5%7D%26%7B1%7D%5C%5C-%7B1%7D%26%7B4%7D%26-%7B3%7D%5C%5C%7B3%7D%26%7B0%7D%26%7B2%7D%7D%5Cright%5D%7D)
somando a transposta de A com 
obtemos a matriz ![[[2x+y,5x+y,8/3],[16/3,8/3,1], [0,-3,4/3]]](http://sga.uniube.br/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7B%5Cleft%5B%5Cmatrix%7B%7B2%7D%7Bx%7D%2B%7By%7D%26%7B5%7D%7Bx%7D%2B%7By%7D%26%5Cfrac%7B%7B8%7D%7D%7B%7B3%7D%7D%5C%5C%5Cfrac%7B%7B16%7D%7D%7B%7B3%7D%7D%26%5Cfrac%7B%7B8%7D%7D%7B%7B3%7D%7D%26%7B1%7D%5C%5C%7B0%7D%26-%7B3%7D%26%5Cfrac%7B%7B4%7D%7D%7B%7B3%7D%7D%7D%5Cright%5D%7D)
A soma dos valores de x +y é igual a:




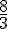
Uma determinada motocicleta sofre uma desvalorização após t anos de sua aquisição, seguindo a função %7D%3D%7BV%7D_%7B%7B0%7D%7D.%7B%7B%5Cleft(%5Cfrac%7B%7B4%7D%7D%7B%7B3%7D%7D%5Cright)%7D%7D%5E%7B%7B-%7B0%7D%2C%7B25%7D%7Bt%7D%7D%7D) , em que
, em que 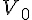 corresponde ao valor de aquisição. Se o preço de aquisição foi de R$ 7 111, 00 então o valor após 8 anos será; aproximadamente:
corresponde ao valor de aquisição. Se o preço de aquisição foi de R$ 7 111, 00 então o valor após 8 anos será; aproximadamente:
3000
4000
5000
2000
6000
Um artesão resolveu incrementar sua produção investindo R$ 300,00 na compra de matéria-prima para confeccionar certo tipo de produto ao preço de custo de R$ 10,00 a unidade (para produzir no máximo 100 unidades), com a intenção de vender cada produto ao preço de R$ 25,00. Podemos afirmar que:
I. O artesão terá lucro quando vender mais de 20 produtos.
II. Ao vender 75 produtos a receita será de R$ 1900,00.
III. O custo para produzir 100 unidades será de exatamente R$1200,00.
IV. O artesão terá lucro de R$ 1200,00 quando vender de 100 unidades.
Está correto o que se afirma em
II e IV.
II e III.
I e IV.
III e IV.
I e II.
Dado o sistema de equações lineares  , podemos afirmar que
, podemos afirmar que
y+z=-10
x=z+1
x+y=7
x=2y
z=4y
Resolva o sistema de equações lineares e classifique-o
S={(z +2,z-1,1). O sistema é possível e indeterminado
S={(1,0,2). O sistema é possível e determinado
S={ }. O sistema é impossível.
S={(1,1,1). O sistema é possível e determinado
S={(3,2,1). O sistema é possível e determinado
Em um laboratório de análises clínicas a temperatura C, em graus Celsius, varia em função do tempo t, em horas, obedecendo a lei matemática C(t) = t² – 4t + 3 . Para a realização de determinado exame é exigido que a temperatura a não chegue a -2Cº. Nessas condições, é possível realizar o referido exame e se sim, qual será a temperatura?
A temperatura mínima atingida será -3, logo o exame poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -0,5, logo o exame poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -3, logo o exame não poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -1, logo o exame poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -0,75, logo o exame poderá ser realizado no referido laboratório.
25°.
13°.
10°.
8°.
15°.
Uma equação modular é toda equação cuja incógnita se apresenta em módulo, considere a equação a seguir
O conjunto solução que satisfaz a equação é dado por:
S = { } (vazio)
S = {-3, -1, 2, 3}
S = {-3, -2, 1, 2}
S = {-1, 1, 2}
S = {-2, 1, 2}
A população da bactéria de uma colônia E. coli dobra a cada 20 minutos. Em um experimento, colocou-se, inicialmente em um tubo de ensaio, uma amostra com 1000 bactérias por milímetro. No final do experimento obteve -se um total de 4,096 . 106 bactérias por milímetro.
Assim sendo, o tempo do experimento foi de
2 horas e 40 minutos.
3 horas.
3 horas e 20 minutos.
3 horas e 40 minutos.
4 horas.
O número de bactérias de certa cultura aumenta exponencialmente conforme a lei de formação %7D%3D%7BQ%7D_%7B%7B0%7D%7D.%7B%7Be%7D%7D%5E%7B%7B%7Bk%7D%7Bt%7D%7D%7D) , onde
, onde  é a quantidade inicial de bactérias ,
é a quantidade inicial de bactérias ,  o número irracional , k é uma constante e t o tempo, em horas, após o início do experimento.
o número irracional , k é uma constante e t o tempo, em horas, após o início do experimento.
Considerando k = 2.
Se uma cultura tem inicialmente 10000 bactérias então 1h depois, terá aproximadamente:
62046 bactérias
39206 bactérias
73891 bactérias
80312 bactérias
100002 bactérias
Dada a matriz, ![[[2, 5, 1],[-1, 4, -3],[3, 0, 2]]](http://sga.uniube.br/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7B%5Cleft%5B%5Cmatrix%7B%7B2%7D%26%7B5%7D%26%7B1%7D%5C%5C-%7B1%7D%26%7B4%7D%26-%7B3%7D%5C%5C%7B3%7D%26%7B0%7D%26%7B2%7D%7D%5Cright%5D%7D)
somando a transposta de A com 
obtemos a matriz ![[[2x+y,5x+y,8/3],[16/3,8/3,1], [0,-3,4/3]]](http://sga.uniube.br/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7B%5Cleft%5B%5Cmatrix%7B%7B2%7D%7Bx%7D%2B%7By%7D%26%7B5%7D%7Bx%7D%2B%7By%7D%26%5Cfrac%7B%7B8%7D%7D%7B%7B3%7D%7D%5C%5C%5Cfrac%7B%7B16%7D%7D%7B%7B3%7D%7D%26%5Cfrac%7B%7B8%7D%7D%7B%7B3%7D%7D%26%7B1%7D%5C%5C%7B0%7D%26-%7B3%7D%26%5Cfrac%7B%7B4%7D%7D%7B%7B3%7D%7D%7D%5Cright%5D%7D)
A soma dos valores de x +y é igual a:




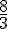
Uma determinada motocicleta sofre uma desvalorização após t anos de sua aquisição, seguindo a função %7D%3D%7BV%7D_%7B%7B0%7D%7D.%7B%7B%5Cleft(%5Cfrac%7B%7B4%7D%7D%7B%7B3%7D%7D%5Cright)%7D%7D%5E%7B%7B-%7B0%7D%2C%7B25%7D%7Bt%7D%7D%7D) , em que
, em que 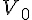 corresponde ao valor de aquisição. Se o preço de aquisição foi de R$ 7 111, 00 então o valor após 8 anos será; aproximadamente:
corresponde ao valor de aquisição. Se o preço de aquisição foi de R$ 7 111, 00 então o valor após 8 anos será; aproximadamente:
3000
4000
5000
2000
6000
Um artesão resolveu incrementar sua produção investindo R$ 300,00 na compra de matéria-prima para confeccionar certo tipo de produto ao preço de custo de R$ 10,00 a unidade (para produzir no máximo 100 unidades), com a intenção de vender cada produto ao preço de R$ 25,00. Podemos afirmar que:
I. O artesão terá lucro quando vender mais de 20 produtos.
II. Ao vender 75 produtos a receita será de R$ 1900,00.
III. O custo para produzir 100 unidades será de exatamente R$1200,00.
IV. O artesão terá lucro de R$ 1200,00 quando vender de 100 unidades.
Está correto o que se afirma em
II e IV.
II e III.
I e IV.
III e IV.
I e II.
Dado o sistema de equações lineares  , podemos afirmar que
, podemos afirmar que
y+z=-10
x=z+1
x+y=7
x=2y
z=4y
Resolva o sistema de equações lineares e classifique-o
S={(z +2,z-1,1). O sistema é possível e indeterminado
S={(1,0,2). O sistema é possível e determinado
S={ }. O sistema é impossível.
S={(1,1,1). O sistema é possível e determinado
S={(3,2,1). O sistema é possível e determinado
Em um laboratório de análises clínicas a temperatura C, em graus Celsius, varia em função do tempo t, em horas, obedecendo a lei matemática C(t) = t² – 4t + 3 . Para a realização de determinado exame é exigido que a temperatura a não chegue a -2Cº. Nessas condições, é possível realizar o referido exame e se sim, qual será a temperatura?
A temperatura mínima atingida será -3, logo o exame poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -0,5, logo o exame poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -3, logo o exame não poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -1, logo o exame poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -0,75, logo o exame poderá ser realizado no referido laboratório.
S = { } (vazio)
S = {-3, -1, 2, 3}
S = {-3, -2, 1, 2}
S = {-1, 1, 2}
S = {-2, 1, 2}
A população da bactéria de uma colônia E. coli dobra a cada 20 minutos. Em um experimento, colocou-se, inicialmente em um tubo de ensaio, uma amostra com 1000 bactérias por milímetro. No final do experimento obteve -se um total de 4,096 . 106 bactérias por milímetro.
Assim sendo, o tempo do experimento foi de
2 horas e 40 minutos.
3 horas.
3 horas e 20 minutos.
3 horas e 40 minutos.
4 horas.
O número de bactérias de certa cultura aumenta exponencialmente conforme a lei de formação %7D%3D%7BQ%7D_%7B%7B0%7D%7D.%7B%7Be%7D%7D%5E%7B%7B%7Bk%7D%7Bt%7D%7D%7D) , onde
, onde  é a quantidade inicial de bactérias ,
é a quantidade inicial de bactérias ,  o número irracional , k é uma constante e t o tempo, em horas, após o início do experimento.
o número irracional , k é uma constante e t o tempo, em horas, após o início do experimento.
Considerando k = 2.
Se uma cultura tem inicialmente 10000 bactérias então 1h depois, terá aproximadamente:
62046 bactérias
39206 bactérias
73891 bactérias
80312 bactérias
100002 bactérias
Dada a matriz, ![[[2, 5, 1],[-1, 4, -3],[3, 0, 2]]](http://sga.uniube.br/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7B%5Cleft%5B%5Cmatrix%7B%7B2%7D%26%7B5%7D%26%7B1%7D%5C%5C-%7B1%7D%26%7B4%7D%26-%7B3%7D%5C%5C%7B3%7D%26%7B0%7D%26%7B2%7D%7D%5Cright%5D%7D)
somando a transposta de A com 
obtemos a matriz ![[[2x+y,5x+y,8/3],[16/3,8/3,1], [0,-3,4/3]]](http://sga.uniube.br/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7B%5Cleft%5B%5Cmatrix%7B%7B2%7D%7Bx%7D%2B%7By%7D%26%7B5%7D%7Bx%7D%2B%7By%7D%26%5Cfrac%7B%7B8%7D%7D%7B%7B3%7D%7D%5C%5C%5Cfrac%7B%7B16%7D%7D%7B%7B3%7D%7D%26%5Cfrac%7B%7B8%7D%7D%7B%7B3%7D%7D%26%7B1%7D%5C%5C%7B0%7D%26-%7B3%7D%26%5Cfrac%7B%7B4%7D%7D%7B%7B3%7D%7D%7D%5Cright%5D%7D)
A soma dos valores de x +y é igual a:




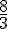
Uma determinada motocicleta sofre uma desvalorização após t anos de sua aquisição, seguindo a função %7D%3D%7BV%7D_%7B%7B0%7D%7D.%7B%7B%5Cleft(%5Cfrac%7B%7B4%7D%7D%7B%7B3%7D%7D%5Cright)%7D%7D%5E%7B%7B-%7B0%7D%2C%7B25%7D%7Bt%7D%7D%7D) , em que
, em que 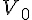 corresponde ao valor de aquisição. Se o preço de aquisição foi de R$ 7 111, 00 então o valor após 8 anos será; aproximadamente:
corresponde ao valor de aquisição. Se o preço de aquisição foi de R$ 7 111, 00 então o valor após 8 anos será; aproximadamente:
3000
4000
5000
2000
6000
Um artesão resolveu incrementar sua produção investindo R$ 300,00 na compra de matéria-prima para confeccionar certo tipo de produto ao preço de custo de R$ 10,00 a unidade (para produzir no máximo 100 unidades), com a intenção de vender cada produto ao preço de R$ 25,00. Podemos afirmar que:
I. O artesão terá lucro quando vender mais de 20 produtos.
II. Ao vender 75 produtos a receita será de R$ 1900,00.
III. O custo para produzir 100 unidades será de exatamente R$1200,00.
IV. O artesão terá lucro de R$ 1200,00 quando vender de 100 unidades.
Está correto o que se afirma em
II e IV.
II e III.
I e IV.
III e IV.
I e II.
Dado o sistema de equações lineares  , podemos afirmar que
, podemos afirmar que
y+z=-10
x=z+1
x+y=7
x=2y
z=4y
Resolva o sistema de equações lineares e classifique-o
S={(z +2,z-1,1). O sistema é possível e indeterminado
S={(1,0,2). O sistema é possível e determinado
S={ }. O sistema é impossível.
S={(1,1,1). O sistema é possível e determinado
S={(3,2,1). O sistema é possível e determinado
Em um laboratório de análises clínicas a temperatura C, em graus Celsius, varia em função do tempo t, em horas, obedecendo a lei matemática C(t) = t² – 4t + 3 . Para a realização de determinado exame é exigido que a temperatura a não chegue a -2Cº. Nessas condições, é possível realizar o referido exame e se sim, qual será a temperatura?
A temperatura mínima atingida será -3, logo o exame poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -0,5, logo o exame poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -3, logo o exame não poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -1, logo o exame poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -0,75, logo o exame poderá ser realizado no referido laboratório.
2 horas e 40 minutos.
3 horas.
3 horas e 20 minutos.
3 horas e 40 minutos.
4 horas.
O número de bactérias de certa cultura aumenta exponencialmente conforme a lei de formação %7D%3D%7BQ%7D_%7B%7B0%7D%7D.%7B%7Be%7D%7D%5E%7B%7B%7Bk%7D%7Bt%7D%7D%7D) , onde
, onde  é a quantidade inicial de bactérias ,
é a quantidade inicial de bactérias ,  o número irracional , k é uma constante e t o tempo, em horas, após o início do experimento.
o número irracional , k é uma constante e t o tempo, em horas, após o início do experimento.
Considerando k = 2.
Se uma cultura tem inicialmente 10000 bactérias então 1h depois, terá aproximadamente:
62046 bactérias
39206 bactérias
73891 bactérias
80312 bactérias
100002 bactérias
Dada a matriz, ![[[2, 5, 1],[-1, 4, -3],[3, 0, 2]]](http://sga.uniube.br/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7B%5Cleft%5B%5Cmatrix%7B%7B2%7D%26%7B5%7D%26%7B1%7D%5C%5C-%7B1%7D%26%7B4%7D%26-%7B3%7D%5C%5C%7B3%7D%26%7B0%7D%26%7B2%7D%7D%5Cright%5D%7D)
somando a transposta de A com 
obtemos a matriz ![[[2x+y,5x+y,8/3],[16/3,8/3,1], [0,-3,4/3]]](http://sga.uniube.br/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7B%5Cleft%5B%5Cmatrix%7B%7B2%7D%7Bx%7D%2B%7By%7D%26%7B5%7D%7Bx%7D%2B%7By%7D%26%5Cfrac%7B%7B8%7D%7D%7B%7B3%7D%7D%5C%5C%5Cfrac%7B%7B16%7D%7D%7B%7B3%7D%7D%26%5Cfrac%7B%7B8%7D%7D%7B%7B3%7D%7D%26%7B1%7D%5C%5C%7B0%7D%26-%7B3%7D%26%5Cfrac%7B%7B4%7D%7D%7B%7B3%7D%7D%7D%5Cright%5D%7D)
A soma dos valores de x +y é igual a:




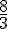
Uma determinada motocicleta sofre uma desvalorização após t anos de sua aquisição, seguindo a função %7D%3D%7BV%7D_%7B%7B0%7D%7D.%7B%7B%5Cleft(%5Cfrac%7B%7B4%7D%7D%7B%7B3%7D%7D%5Cright)%7D%7D%5E%7B%7B-%7B0%7D%2C%7B25%7D%7Bt%7D%7D%7D) , em que
, em que 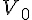 corresponde ao valor de aquisição. Se o preço de aquisição foi de R$ 7 111, 00 então o valor após 8 anos será; aproximadamente:
corresponde ao valor de aquisição. Se o preço de aquisição foi de R$ 7 111, 00 então o valor após 8 anos será; aproximadamente:
3000
4000
5000
2000
6000
Um artesão resolveu incrementar sua produção investindo R$ 300,00 na compra de matéria-prima para confeccionar certo tipo de produto ao preço de custo de R$ 10,00 a unidade (para produzir no máximo 100 unidades), com a intenção de vender cada produto ao preço de R$ 25,00. Podemos afirmar que:
I. O artesão terá lucro quando vender mais de 20 produtos.
II. Ao vender 75 produtos a receita será de R$ 1900,00.
III. O custo para produzir 100 unidades será de exatamente R$1200,00.
IV. O artesão terá lucro de R$ 1200,00 quando vender de 100 unidades.
Está correto o que se afirma em
II e IV.
II e III.
I e IV.
III e IV.
I e II.
Dado o sistema de equações lineares  , podemos afirmar que
, podemos afirmar que
y+z=-10
x=z+1
x+y=7
x=2y
z=4y
Resolva o sistema de equações lineares e classifique-o
S={(z +2,z-1,1). O sistema é possível e indeterminado
S={(1,0,2). O sistema é possível e determinado
S={ }. O sistema é impossível.
S={(1,1,1). O sistema é possível e determinado
S={(3,2,1). O sistema é possível e determinado
Em um laboratório de análises clínicas a temperatura C, em graus Celsius, varia em função do tempo t, em horas, obedecendo a lei matemática C(t) = t² – 4t + 3 . Para a realização de determinado exame é exigido que a temperatura a não chegue a -2Cº. Nessas condições, é possível realizar o referido exame e se sim, qual será a temperatura?
A temperatura mínima atingida será -3, logo o exame poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -0,5, logo o exame poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -3, logo o exame não poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -1, logo o exame poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -0,75, logo o exame poderá ser realizado no referido laboratório.
62046 bactérias
39206 bactérias
73891 bactérias
80312 bactérias
100002 bactérias
Dada a matriz, ![[[2, 5, 1],[-1, 4, -3],[3, 0, 2]]](http://sga.uniube.br/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7B%5Cleft%5B%5Cmatrix%7B%7B2%7D%26%7B5%7D%26%7B1%7D%5C%5C-%7B1%7D%26%7B4%7D%26-%7B3%7D%5C%5C%7B3%7D%26%7B0%7D%26%7B2%7D%7D%5Cright%5D%7D)
somando a transposta de A com 
obtemos a matriz ![[[2x+y,5x+y,8/3],[16/3,8/3,1], [0,-3,4/3]]](http://sga.uniube.br/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7B%5Cleft%5B%5Cmatrix%7B%7B2%7D%7Bx%7D%2B%7By%7D%26%7B5%7D%7Bx%7D%2B%7By%7D%26%5Cfrac%7B%7B8%7D%7D%7B%7B3%7D%7D%5C%5C%5Cfrac%7B%7B16%7D%7D%7B%7B3%7D%7D%26%5Cfrac%7B%7B8%7D%7D%7B%7B3%7D%7D%26%7B1%7D%5C%5C%7B0%7D%26-%7B3%7D%26%5Cfrac%7B%7B4%7D%7D%7B%7B3%7D%7D%7D%5Cright%5D%7D)
A soma dos valores de x +y é igual a:




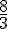
Uma determinada motocicleta sofre uma desvalorização após t anos de sua aquisição, seguindo a função %7D%3D%7BV%7D_%7B%7B0%7D%7D.%7B%7B%5Cleft(%5Cfrac%7B%7B4%7D%7D%7B%7B3%7D%7D%5Cright)%7D%7D%5E%7B%7B-%7B0%7D%2C%7B25%7D%7Bt%7D%7D%7D) , em que
, em que 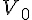 corresponde ao valor de aquisição. Se o preço de aquisição foi de R$ 7 111, 00 então o valor após 8 anos será; aproximadamente:
corresponde ao valor de aquisição. Se o preço de aquisição foi de R$ 7 111, 00 então o valor após 8 anos será; aproximadamente:
3000
4000
5000
2000
6000
Um artesão resolveu incrementar sua produção investindo R$ 300,00 na compra de matéria-prima para confeccionar certo tipo de produto ao preço de custo de R$ 10,00 a unidade (para produzir no máximo 100 unidades), com a intenção de vender cada produto ao preço de R$ 25,00. Podemos afirmar que:
I. O artesão terá lucro quando vender mais de 20 produtos.
II. Ao vender 75 produtos a receita será de R$ 1900,00.
III. O custo para produzir 100 unidades será de exatamente R$1200,00.
IV. O artesão terá lucro de R$ 1200,00 quando vender de 100 unidades.
Está correto o que se afirma em
II e IV.
II e III.
I e IV.
III e IV.
I e II.
Dado o sistema de equações lineares  , podemos afirmar que
, podemos afirmar que
y+z=-10
x=z+1
x+y=7
x=2y
z=4y
Resolva o sistema de equações lineares e classifique-o
S={(z +2,z-1,1). O sistema é possível e indeterminado
S={(1,0,2). O sistema é possível e determinado
S={ }. O sistema é impossível.
S={(1,1,1). O sistema é possível e determinado
S={(3,2,1). O sistema é possível e determinado
Em um laboratório de análises clínicas a temperatura C, em graus Celsius, varia em função do tempo t, em horas, obedecendo a lei matemática C(t) = t² – 4t + 3 . Para a realização de determinado exame é exigido que a temperatura a não chegue a -2Cº. Nessas condições, é possível realizar o referido exame e se sim, qual será a temperatura?
A temperatura mínima atingida será -3, logo o exame poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -0,5, logo o exame poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -3, logo o exame não poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -1, logo o exame poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -0,75, logo o exame poderá ser realizado no referido laboratório.
Uma determinada motocicleta sofre uma desvalorização após t anos de sua aquisição, seguindo a função %7D%3D%7BV%7D_%7B%7B0%7D%7D.%7B%7B%5Cleft(%5Cfrac%7B%7B4%7D%7D%7B%7B3%7D%7D%5Cright)%7D%7D%5E%7B%7B-%7B0%7D%2C%7B25%7D%7Bt%7D%7D%7D) , em que
, em que 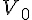 corresponde ao valor de aquisição. Se o preço de aquisição foi de R$ 7 111, 00 então o valor após 8 anos será; aproximadamente:
corresponde ao valor de aquisição. Se o preço de aquisição foi de R$ 7 111, 00 então o valor após 8 anos será; aproximadamente:
3000
4000
5000
2000
6000
Um artesão resolveu incrementar sua produção investindo R$ 300,00 na compra de matéria-prima para confeccionar certo tipo de produto ao preço de custo de R$ 10,00 a unidade (para produzir no máximo 100 unidades), com a intenção de vender cada produto ao preço de R$ 25,00. Podemos afirmar que:
I. O artesão terá lucro quando vender mais de 20 produtos.
II. Ao vender 75 produtos a receita será de R$ 1900,00.
III. O custo para produzir 100 unidades será de exatamente R$1200,00.
IV. O artesão terá lucro de R$ 1200,00 quando vender de 100 unidades.
Está correto o que se afirma em
II e IV.
II e III.
I e IV.
III e IV.
I e II.
Dado o sistema de equações lineares  , podemos afirmar que
, podemos afirmar que
y+z=-10
x=z+1
x+y=7
x=2y
z=4y
Resolva o sistema de equações lineares e classifique-o
S={(z +2,z-1,1). O sistema é possível e indeterminado
S={(1,0,2). O sistema é possível e determinado
S={ }. O sistema é impossível.
S={(1,1,1). O sistema é possível e determinado
S={(3,2,1). O sistema é possível e determinado
Em um laboratório de análises clínicas a temperatura C, em graus Celsius, varia em função do tempo t, em horas, obedecendo a lei matemática C(t) = t² – 4t + 3 . Para a realização de determinado exame é exigido que a temperatura a não chegue a -2Cº. Nessas condições, é possível realizar o referido exame e se sim, qual será a temperatura?
A temperatura mínima atingida será -3, logo o exame poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -0,5, logo o exame poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -3, logo o exame não poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -1, logo o exame poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -0,75, logo o exame poderá ser realizado no referido laboratório.
3000
4000
5000
2000
6000
Um artesão resolveu incrementar sua produção investindo R$ 300,00 na compra de matéria-prima para confeccionar certo tipo de produto ao preço de custo de R$ 10,00 a unidade (para produzir no máximo 100 unidades), com a intenção de vender cada produto ao preço de R$ 25,00. Podemos afirmar que:
I. O artesão terá lucro quando vender mais de 20 produtos.
II. Ao vender 75 produtos a receita será de R$ 1900,00.
III. O custo para produzir 100 unidades será de exatamente R$1200,00.
IV. O artesão terá lucro de R$ 1200,00 quando vender de 100 unidades.
Está correto o que se afirma em
II e IV.
II e III.
I e IV.
III e IV.
I e II.
Dado o sistema de equações lineares  , podemos afirmar que
, podemos afirmar que
y+z=-10
x=z+1
x+y=7
x=2y
z=4y
Resolva o sistema de equações lineares e classifique-o
S={(z +2,z-1,1). O sistema é possível e indeterminado
S={(1,0,2). O sistema é possível e determinado
S={ }. O sistema é impossível.
S={(1,1,1). O sistema é possível e determinado
S={(3,2,1). O sistema é possível e determinado
Em um laboratório de análises clínicas a temperatura C, em graus Celsius, varia em função do tempo t, em horas, obedecendo a lei matemática C(t) = t² – 4t + 3 . Para a realização de determinado exame é exigido que a temperatura a não chegue a -2Cº. Nessas condições, é possível realizar o referido exame e se sim, qual será a temperatura?
A temperatura mínima atingida será -3, logo o exame poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -0,5, logo o exame poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -3, logo o exame não poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -1, logo o exame poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -0,75, logo o exame poderá ser realizado no referido laboratório.
II e IV.
II e III.
I e IV.
III e IV.
I e II.
Dado o sistema de equações lineares  , podemos afirmar que
, podemos afirmar que
y+z=-10
x=z+1
x+y=7
x=2y
z=4y
Resolva o sistema de equações lineares e classifique-o
S={(z +2,z-1,1). O sistema é possível e indeterminado
S={(1,0,2). O sistema é possível e determinado
S={ }. O sistema é impossível.
S={(1,1,1). O sistema é possível e determinado
S={(3,2,1). O sistema é possível e determinado
Em um laboratório de análises clínicas a temperatura C, em graus Celsius, varia em função do tempo t, em horas, obedecendo a lei matemática C(t) = t² – 4t + 3 . Para a realização de determinado exame é exigido que a temperatura a não chegue a -2Cº. Nessas condições, é possível realizar o referido exame e se sim, qual será a temperatura?
A temperatura mínima atingida será -3, logo o exame poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -0,5, logo o exame poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -3, logo o exame não poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -1, logo o exame poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -0,75, logo o exame poderá ser realizado no referido laboratório.
y+z=-10
x=z+1
x+y=7
x=2y
z=4y
Resolva o sistema de equações lineares e classifique-o
S={(z +2,z-1,1). O sistema é possível e indeterminado
S={(1,0,2). O sistema é possível e determinado
S={ }. O sistema é impossível.
S={(1,1,1). O sistema é possível e determinado
S={(3,2,1). O sistema é possível e determinado
Em um laboratório de análises clínicas a temperatura C, em graus Celsius, varia em função do tempo t, em horas, obedecendo a lei matemática C(t) = t² – 4t + 3 . Para a realização de determinado exame é exigido que a temperatura a não chegue a -2Cº. Nessas condições, é possível realizar o referido exame e se sim, qual será a temperatura?
A temperatura mínima atingida será -3, logo o exame poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -0,5, logo o exame poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -3, logo o exame não poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -1, logo o exame poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -0,75, logo o exame poderá ser realizado no referido laboratório.
S={(z +2,z-1,1). O sistema é possível e indeterminado
S={(1,0,2). O sistema é possível e determinado
S={ }. O sistema é impossível.
S={(1,1,1). O sistema é possível e determinado
S={(3,2,1). O sistema é possível e determinado
Em um laboratório de análises clínicas a temperatura C, em graus Celsius, varia em função do tempo t, em horas, obedecendo a lei matemática C(t) = t² – 4t + 3 . Para a realização de determinado exame é exigido que a temperatura a não chegue a -2Cº. Nessas condições, é possível realizar o referido exame e se sim, qual será a temperatura?
A temperatura mínima atingida será -3, logo o exame poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -0,5, logo o exame poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -3, logo o exame não poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -1, logo o exame poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -0,75, logo o exame poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -3, logo o exame poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -0,5, logo o exame poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -3, logo o exame não poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -1, logo o exame poderá ser realizado no referido laboratório.
A temperatura mínima atingida será -0,75, logo o exame poderá ser realizado no referido laboratório.